算法代写|COMP3027 & COMP3927 Algorithm Design Assignment 3
这是一个算法设计的CS代写案例
Problem 1. (20 points)
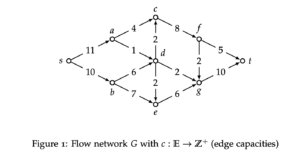
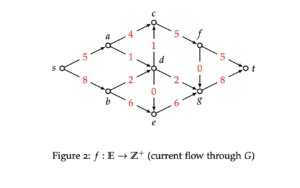
To begin, let us consider the Ford-Fulkerson algorithm. Consider below the flow
network G,c in Figure 1 and the current s−t flow f in Figure 2. Your task is to run one iteration of the Ford-Fulkerson algorithm on the flow network.
- a) Draw the residual graph associated with the flow f. Specify the residual capacity of every edge. You are allowed to draw this by hand and insert a photo (Alternatively, there is a LaTeX template on the last two pages of this assignment that you can use).
- b) Specify an s − t path used to update the flow.
- c) After the update, is the new flow through the network a max flow? Explain
why.
- d) Specify a Min-Cut associated with graph G.
Problem 2. (80 points) (COMP3027 only)
You and your friends have decided to go on a great go-karting adventure. You’ve
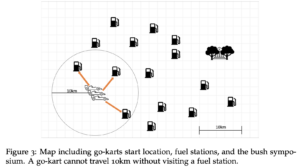
heard that there is to be a symposium for algorithms and computing theory (SACT for short) in the bush (with music!), and since your good friend André owns k go-karts, you decide that the most fun way to get there is via an epic four wheel journey. There is only one issue – the go-karts can only go so far before they need to be refueled, meaning you need to design a trip that allows for picking up fuel every 10km. Even worse, you have realised that all these stops only have enough fuel for one go-kart, meaning that each individual go-kart will need to refuel at different stops. Formally, the SACT Go-Kart Problem is the following; given a positive integer k, n (2D) Cartesian points describing fuel stations and both a starting point S and end point T in the Cartesian plane, determine if k friends have valid paths from S to T. Note that a valid path involves stopping at a fuel station every 10km or less.
Figure 3: Map including go-karts start location, fuel stations, and the bush sympo- sium. A go-kart cannot travel 10km without visiting a fuel station.
As a keen algorithm’s student (after all, you’re trying to get to an algorithms conference!), you realise that the SACT Go-Kart Problem can potentially be solved through the use of flow network algorithms!
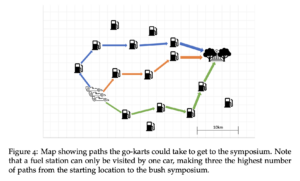
Figure 4: Map showing paths the go-karts could take to get to the symposium. Note that a fuel station can only be visited by one car, making three the highest number of paths from the starting location to the bush symposium.
Your task is to design a reduction from the SACT Go-Kart Problem above to an instance of Max Flow. For full marks, your reduction should be as fast as possible.
- a) Describe how you translate an instance of the SACT Go-Kart Problem into an instance of Max Flow. In particular, you need to describe how you construct the flow network H based on the input of fuel stations, start and end points.
- b) State which algorithm you use to compute the max flow in H.
- c) Describe how you translate the output of the algorithm in (b) into a solution for the SACT Go-Kart Problem. In particular, describe how you determine if all k people are able to make the bush conference, and what their paths would be.
- d) Prove the correctness of your reduction. In particular, you need to prove that there exists an integer F for which the following two statements hold:
• If the max flow is at least F, then your translation procedure in (c) pro- duces feasible paths for all k people.
• If there are feasible paths for all k people, then the max flow is at least F.
- e) Prove the time complexity of your entire reduction, taking into account the steps in parts (a), (b) and (c). Make sure that your time complexity is stated in terms of n and k.