算法代写|COMP3027 & COMP3927 Algorithm Design Assignment 3
这是一个算法设计相关的算法代写案例
Problem 1. (20 points)
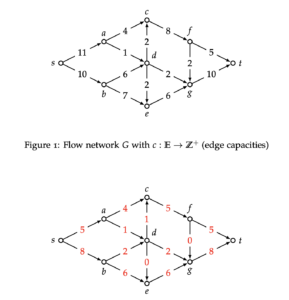
To begin, let us consider the Ford-Fulkerson algorithm. Consider below the flow
network G,c in Figure 1 and the current s−t flow f in Figure 2. Your task is to run one iteration of the Ford-Fulkerson algorithm on the flow network.
- a) Draw the residual graph associated with the flow f. Specify the residual capacity of every edge. You are allowed to draw this by hand and insert a photo.
- b) Specify an s − t path used to update the flow.
- c) After the update, is the new flow through the network a max flow? Explain why.
- d) Specify a Min-Cut associated with graph G.
Problem 2. (80 points) (COMP3027 only)
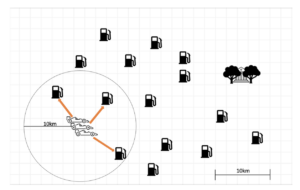
You and your friends have decided to go on a great go-karting adventure. You’ve heard that there is to be a symposium for algorithms and computing theory (SACT for short) in the bush (with music!), and since your good friend André owns k go-karts, you decide that the most fun way to get there is via an epic four wheel journey. There is only one issue – the go-karts can only go so far before they need to be refueled, meaning you need to design a trip that allows for picking up fuel every 10km. Even worse, you have realised that all these stops only have enough fuel for one go-kart, meaning that each individual go-kart will need to refuel at different stops. Formally, the SACT Go-Kart Problem is the following; given a positive integer k, n (2-dimensional) Cartesian points describing fuel stations and both a starting point S and end point T in the Cartesian plane, determine if k friends have valid paths from S to T. Note that a valid path involves stopping at a fuel station every 10km or less.
Figure 3: Map including go-karts start location, fuel stations, and the bush sympo- sium. A go-kart cannot travel 10km without visiting a fuel station.