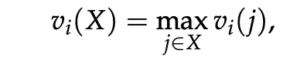CS代写|CSCI 1440/2440 Homework 6: EPIC Auctions
这是一个CS作业代写的相关案例
1.English Auctions
We say that an ascending auction is DSIC up to ε iff no bidder who deviates from sincere bidding can improve upon sincere bidding by more than ε, where ε is the price increment of the auction. Likewise, we can define the notion of any equilibrium “up to ε,” where by deviating from the equilibrium strategy, no bidder can improve their expected utility by more than ε, assuming the other players are conforming. Show by counterexample that the English auction is not DSIC, even up to ε.
Keep in mind that the other bidders need not bid sincerely, and that strategies in the English auction can be outright bizarre: i.e., behavior from one round to the next need not be consistent.
Prove that the English auction is EPIC, up to ε.: i.e., sincere bid- ding is an ex-post Nash equilibrium (EPNE), up to ε.
Apply the Revelation Principle to transform the English auction, in which sincere bidding is an ε-EPNE, into a direct mechanism, which is DSIC/EPIC up to ε. Briefly describe how the Revelation Principle closes the loopholes in the English auction design.
2. Japanese Auctions
This problem concerns Japanese auctions, a variant of the classic English auction that poses demand queries rather than value queries, and that forbids bidders from re-entering after exiting (i.e., skipping even one round of bidding in) the auction.
A k-good Japanese auction for k homogeneous goods can be for- mally specified as follows: Given a fixed price increment ε,
- Initialize the set of bidders S0 = [n] and the price p0 = 0.
- At each round i = 1,2,…,
– Let price pi = iε.
– Let Si be the bidders in Si−1 who remains interested at price pi. N.B. No bidder who expressed disinterest earlier can re-express their interest at some later round.
- Increment i until |Si| ≤ k. Call the final round t.
– Give |St| of the k goods to the bidders in St at price tε.– Give the remaining k − |St| of the goods (if any) to random bidders in St−1 \ St at price (t − 1)ε.
Bidders with unit demand valuations do not demand more than one good. More specifically, their value for any bundle they might be allocated is simply their maximum value across all individual goods: i.e., a bidder i’s valuation is unit demand if their value for a bundle of goods X ⊆ G is given by
- where vi(j) denotes i’s value for good j.
Assuming unit demand valuations, show the following:
The k-good Japanese auction is still not DSIC.
Hint: It suffices to exhibit a counterexample in the single-good
case: i.e., when k = 1.
The k-good Japanese auction is DSIC up to ε.
Online auctions are big business: eBay reported revenue upwards
of $10 billion in 2020! In online auctions, interested bidders report
a “value,” which can be understood as the maximum price they are willing to pay for a good. Valid bids are at least some fixed increment ε greater than the asking price of the good (which is initialized to a reserve price). Whenever a new and valid bid arrives, the auction ten- tatively allocates the good to a bidder with the highest valid bid, and the asking price is updated to the maximum of the second-highest bid and the reserve. (Ties are broken in favor of earlier bidders.)
Although eBay auctions are the most prevalent online auctions in use today, Amazon also ran auctions back in the day.1 The primary difference in rules between eBay and Amazon auctions is that eBay
auctions end at a prespecified time, while Amazon auctions would continue until quiescence: i.e., until a grace period of, say, 24 hours had passed without any active bidding.
Consider the following four types of bidders in online auctions:
- “Truthful” bidders, namely those who bid as if the auction were sealed-bid—they enter their value once and only once, when the auction starts.
- Incremental bidders, who bid on eBay as if it were an English auction—they never enter their value; they merely increment their bid so long as the asking price is below their value.
- Jump bidders, who again bid when the asking price is below their value, placing a bid that is below their value, but more than just the minimal acceptable increment above the current price.
- Snipers (only relevant on eBay, not Amazon), who place a bid no higher than their value once and only once just a few seconds before the auction ends.